|
Caiguda lliure
Se l'anomena
caiguda lliure al moviment que es deu únicament a la influència de
la gravetat.
·
Tots els cossos amb aquest tipus de moviment tenen una acceleració
dirigit cap avall el valor de la qual depèn del lloc en què es
trobin. A la Terra aquest valor és d'aproximadament 9,8 m/s², és a
dir que els cossos deixats en caiguda lliure augmenten la seva
velocitat (cap avall) en 9,8 m/s
cada segon .
·
En la caiguda lliure no es té en compte la resistència de l'aire.
L'acceleració
a què es veu sotmès un cos en caiguda lliure és tan important en la
Física que rep el nom especial d'acceleració
de la gravetat i es representa mitjançant la lletra
g.
| Lloc |
g (m/s²) |
|
Hem dit abans que
l'acceleració d'un cos en caiguda lliure depenia del lloc en què es
trobés. A l'esquerra tens alguns valors aproximats de g en diferents
llocs del nostre Sistema Solar.
Per fer més
còmodes els càlculs de classe solem utilitzar per a l'acceleració de la
gravetat a la Terra el valor aproximat de 10 m/s² en comptes de 9,8 m/s²,
que seria més correcte |
| Mercuri |
2,8 |
| Venus |
8,9 |
| Terra |
9,8 |
| Mart |
3,7 |
| Júpiter |
22,9 |
| Saturn |
9,1 |
| Urà |
7,8 |
| Neptú |
11,0 |
| Lluna |
1,6 |

En el gràfic i
a la taula es pot veure la posició d'un cos en caiguda lliure a
intervals regulars d'1 segon.
Per realitzar
els càlculs s'ha utilitzat el valor g = 10 m/s².
Observa que la
distància recorreguda en cada interval és cada cop major i això és
un signe inequívoc de què la velocitat va augmentant cap avall
| temps (s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| posició (m) |
0 |
-5 |
-20 |
-45 |
-80 |
-125 |
-180 |
-245 |
Ara és un bon
moment per repassar les pàgines que es refereixen a la interpretació
de les gràfiques e-t i v-t i recordar el que hem après sobre elles.
Ja hem vist
que les gràfiques
posició-temps i
velocitat-temps poden
proporcionar-nos molta informació sobre les característiques d'un
moviment.
Per a la
caiguda lliure, la gràfica posició temps té l'aparença següent:
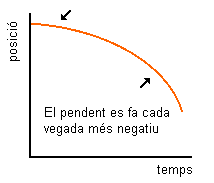
Recorda que en
les gràfiques posició-temps, una corba indicava l'existència
d'acceleració.
El pendent
cada cop més negativa ens indica que la velocitat del cos és cada
cop més negativa, és a dir cada cop major però dirigit cap avall.
Això significa que el moviment es va fent més ràpid a mesura que
transcorre el temps.
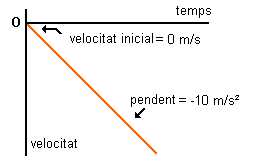
Observa la
gràfica v-t de la dreta que correspon a un moviment de caiguda
lliure.
La seva forma
recta ens indica que l'acceleració és constant, és a dir que la
variació de la velocitat en intervals regulars de temps és constant.
| temps (s) |
0 |
1 |
2 |
3 |
4 |
5 |
| velocitat (m/s) |
0 |
-10 |
-20 |
-30 |
-40 |
-50 |
El pendent
negatiu ens indica que l'acceleració és negativa. A la taula
anterior podem veure que la variació de la velocitat a intervals
d'un segon és sempre la mateixa (-10 m/s). Això vol dir que
l'acceleració per a qualsevol dels intervals de temps és:
g
= -10 m/s / 1s = -10 m/s/s = -10 m/s²
Equacions per a la caiguda lliure
Recorda les
equacions generals del moviment:
e =
vo·t +
½·a·t²
vf =
vo +
a·t
Podem adaptar
aquestes equacions per al moviment de caiguda lliure. Si suposem que
deixem caure un cos (en comptes de llançar-ho), llavors la seva
velocitat inicial serà zero i per tant el primer sumand de cadascuna
de les equacions anteriors també serà zero, i podem eliminar-los:
e = ½·a·t²
vf = a·t
D'altra banda,
en una caiguda lliure la posició que ocupa el cos en un instant és
precisament la seva altura h en
aquest moment.
Com hem quedat
a anomenar g a l'acceleració que
experimenta un cos en caiguda lliure, podem expressar les equacions
així:
h = ½·g·t²
vf =
g·t
Una contradicció?
Si has estudiat amb
atenció aquesta pàgina, estaràs sorprès perquè hem començat dient que
l'acceleració de la gravetat té un valor a la Terra de
10 m/s² i, no obstant això, en realitzar
l'estudi gràfic hem arribat a la conclusió que es tractava d'un valor
negatiu: -10 m/s².
Recorda que totes les
observacions que fem sobre les característiques d'un moviment depenen del
sistema de referència elegit (generalment la Terra).
A vegades ens
interessa canviar el nostre sistema de referència per expressar les dades
amb major comoditat 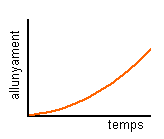
En el cas de la
caiguda lliure, sembla lògic situar el sistema de referència en la posició
inicial del cos per mesurar l'allunyament que experimenta i assignar
valors positius a les distàncies recorregut cap
avall.
| temps (s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| posició (m) |
0 |
5 |
20 |
45 |
80 |
125 |
180 |
245 |
Això significa que ara
estem considerant sentit positiu cap avall i sentit negatiu cap amunt, per
la qual cosa la gràfica posició-temps seria com l'anterior.
De la nova gràfica
posició-temps deduïm que ara la velocitat és positiva (cap avall) i cada cop
major perquè el pendent és positiva i cada cop major.
El valor que obtenim
ara per a g és +10 m/s², però no es tracta d'una contradicció.
Recorda que hi ha un
conveni per interpretar quin sentit té l'acceleració:
Si el mòbil està
disminuint la seva rapidesa (està frenant), llavors la seva acceleració va
en el sentit contrari al moviment.
Si el mòbil augmenta
la seva rapidesa, l'acceleració té el mateix sentit que la velocitat.
Si apliquem aquest
conveni ens adonem que el sentit de g no ha
canviat: continua sent cap avall.
El següent applet
simula la caiguda lliure d'un cos en diferents condicions de gravetat i
dibuixa les gràfiques v-t que corresponen al nostre nou sistema de
referència. Es tracta d'un cos que porta enganxada una tira de paper sobre
la qual un dispositiu realitza marques a intervals regulars de temps:
Hauràs
observat en treballar amb l'applet que les gràfiques v-t canvien en
modificar els valors de g però no
ocorre el mateix si variem la massa
del cos.
Potser això
et sembli estrany però no oblidis que només diem caiguda lliure al
moviment que únicament està influït per la gravetat.
Si
tinguéssim en compte la resistència de l'aire, sí que tindrien
importància la massa i la forma del cos, però
no es tractaria d'una caiguda lliure.
Per cert,
sabries determinar l'escala utilitzada en l'applet per al temps i la
velocitat?
Pujar en caiguda lliure?
Doncs sí!
Si llancem
un cos verticalment cap amunt, arribarà una altura màxima i després
caurà. Tant la fase de pujada com la de baixada són de caiguda
lliure perquè així anomenem als moviments que només depenen de la
gravetat.
Mentre el
cos va cap amunt, la seva rapidesa disminueix i per tant la gravetat
estarà dirigida en sentit contrari, és a dir cap avall.
Vegem un
exemple:
Suposa que
estem a la Lluna i llancem un cos verticalment cap amunt amb una
rapidesa de 30 m/s, quina altura màxima aconseguirà?
En trobar-nos
a la Lluna, utilitzarem el valor de g que apareix a la taula. Com la
rapidesa del moviment anirà
disminuint fins a fer-se zero en el
punt d'altura màxima, la gravetat serà de
sentit contrari al de la velocitat. Així, el valor de la
gravetat que hem d'utilitzar és g = -1,6 m/s².
La
velocitat final és zero ja que és la
velocitat que té el cos quan aconsegueix la seva altura màxima, i
aquest instant és el final del nostre estudi (no ens pregunten el
que ocorre després d'aquest moment)
Esquema:
|
Dades:
|
Cerquem:
|
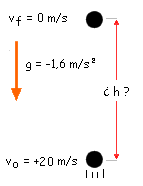
|
vo = +20 m/s
vf = 0 m/s
g = -1,6 m/s²
|
h = ?
|
Per
calcular l'altura hem d'utilitzar l'equació:
h = vo·t +
½·g·t²
però
necessitem saber, prèviament, el temps en què s'aconseguirà
l'altura màxima, per al que utilitzarem l'equació:
vf =
vo + g·t
0 = 20 m/s + (-1,6) m/s²·t
-20 m/s = -1,6 m/s²·t
t
= (-20 m/s)/(-1,6 m/s²) = 12,5 s
Ja
podem calcular l'altura:
h = vo·t +
½·g·t²
h = 20 m/s·12,5 s + 0,5·(-1,6 m/s²)·(12,5 s)²
h
= 250 m - 125 m = 125 m
Aquest
resultat no és exagerat ja que hem fet els càlculs per a la
Luna, on la gravetat és unes sis vegades
menor que a la Terra.
Sabries
calcular, basant-te en aquesta aproximació, l'altura que hagués
aconseguit a la Terra?

|